Homework 2
Getting your assignment: You can find template code for your submission here at this GitHub Classroom link. All of the code you write you should go in hw2.Rmd, and please knit the Markdown file in your completed submission.
Introduction
Neural networks were a revolution in the scientific study of cognitive neuroscience, spawning a large body of work investigating the computational properties of systems designed to model the operation of the brain’s basic computational units (Rosenblatt, 1958. These perceptrons varied along a number of dimensions, but all of them had the same critical flaw: they could not learn non-linear combinations of inputs, leading to their failure on even simple problems like Exclusive Or (XOR; Minsky & Papert, 1967).
In the 1980s, work by David Rumelhart and his colleagues rekindled the field’s interest in neural networks by devising an algorithm by which these models could learn non-linear combinations of input and develop genuinely interesting and surprisingly representations of their input (Rumelhart, Hinton, & Williams, 1986). This lead to an explosion of work in artificial neural networks in the following decades, and also, following Marr’s perspective, a reconsideration of what these models were intended to describe (e.g. the neurons in the networks need not map on to neurons in the brain).
In this assignment you will first implement simple one-layer perceptrons that learn with the perceptron learning rule. You’ll show that these can learn several logical functions: AND, OR, and NOT. But they cannot learn XOR.
You will then build a very simple multi-layer network that uses backpropagation to learn XOR. You’ll finally use the neuralnet package to solve this same problem, and then use it to build a digit classifier using a small version of the MNIST dataset
Perceptrons
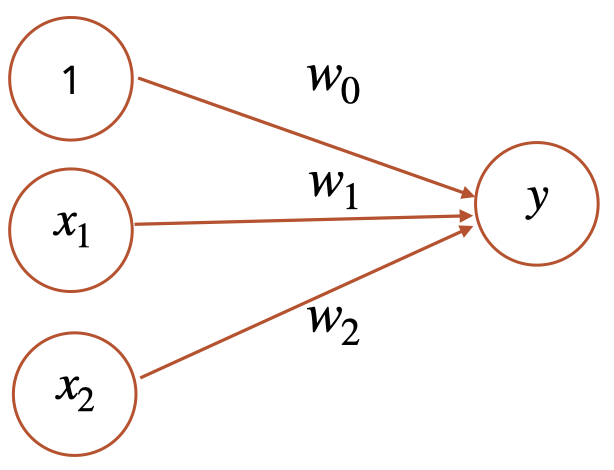
Your first goal will be to train a perceptron to solve logical AND. I’ve provided a set of stub functions that scaffold one way of doing this. The idea is to approximate a sort of pseudo-object oriented structure using a named list. This is overkill for just this simple perceptron, but you’ll find that it extends easily to a backprop network.
This object defined in the perceptron function. A perceptron is a list that has 5 elements:
A
tibbleof inputsA list of target
ys for those inputsA list of
outputs for the last run of the network corresponding to these inputsA list of
activations that occur after applying thesigmoidfunction to thoseoutputsA list of
weights– 3 in total. Two that connect from the input nodes (x1,x2), and one that connects from a bias node (1) to the output node (y).
This list will track the state of the perceptron as it goes through the training function you write (train_perceptron). You can write this function as two nested for loop, the outer one over iterations, and the inner one over examples. In each run of the inner loop, you will
Run
perceptron_feedforwardover the training example.Run
perceptron_feedbackover that training example to update the weights.
In each run of the outer loop, you will run perceptron_feedforward and perceptron_feewdback on all of the examples, and then compute the error for that iteration and store it in the network, e.g. perceptron$errors[iteration] <- sq_error(...).You’ll need to make sure you define perceptron$errors as a list of the right length at the start of the train_perceptron function.
If you want to use these stubs, your plan of attack should be:
Write the helper functions
sigmoidandsq_errorMake the
and_datatibble with columnsx1,x2, andythat corresponds to the four possible input and output combinations for ANDWrite the
perceptron_feedforwardandperceptron_feedbackfunctionsWrite
train_perceptronRun
train_perceptronon your AND data, and plot or otherwise summarize the change in errors over time and the final weights.
Problem 1: Fill out the stub helper functions sigmoid and sq_error (1 point)
Problem 2: Write code to train a perceptron to solve logical AND. You can use the stubs provided in the hw2.Rmd or write your own. Train the perceptron, and report back on the results. Did the error in the network go down over the course of training? What were the final weights? (3 points)
Problem 3: Use your functions to train the perceptron on OR, NOT X1, and XOR. Which problems did it succeed on. Which did it fail on? What were the final weights for each? Do they make sense? (2 points)
Multi-layer networks
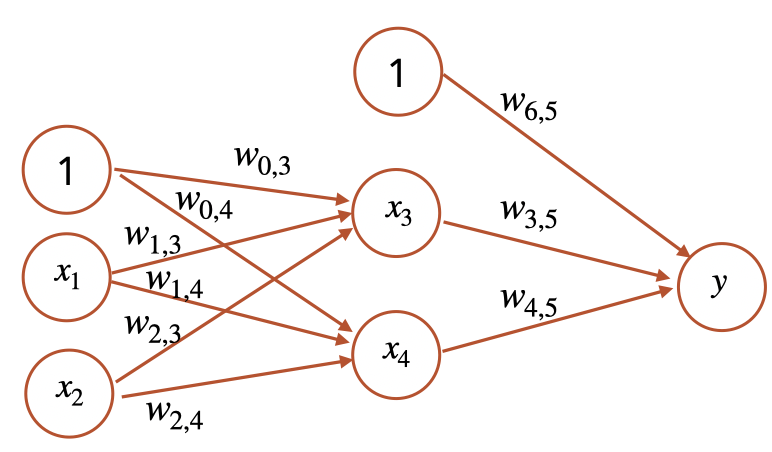
If everything went right, you will have discovered in Problem 3 that perceptrons cannot learn to solve non-linear classification problems like XOR. But with a hidden layer, we can fix this problem. You can use the same strategy you used for your perceptron to implement a 2-layer backpropagation network. You might find the backprop by hand example we did helpful for reference for the weight update formulas.
Using the neuralnet package
The network you implemented is likely to be pretty inefficient. In practice, most implementations of neural networks use matrix multiplication to compute weights and outputs, which drastically speeds things up. For the last two problems, you’ll be using the neuralnet r package to investigate what these networks can learn in a more interesting problem.
The workhorse of the package is the neuralnet function which trains neural nets to solve problems. It uses formula notation just like lm and other standard statistical methods in R.
Problem 5: Use the provided code to run neuralnet on your xor data, and the plot your neuralnet to see what the weights on each node are. Did it learn the same thing as the network you made from scratch?
Now that you understand how this package works, you’ll use it to solve a more interesting classification problem. You’ll be learning to classify handwritten digits from the MNIST dataset that are a classic success story for modern neural networks. You’ll be working with just a small, scaled down subset of the real dataset — 100 examples of each of the digits 0-9. Here is the first example of each:
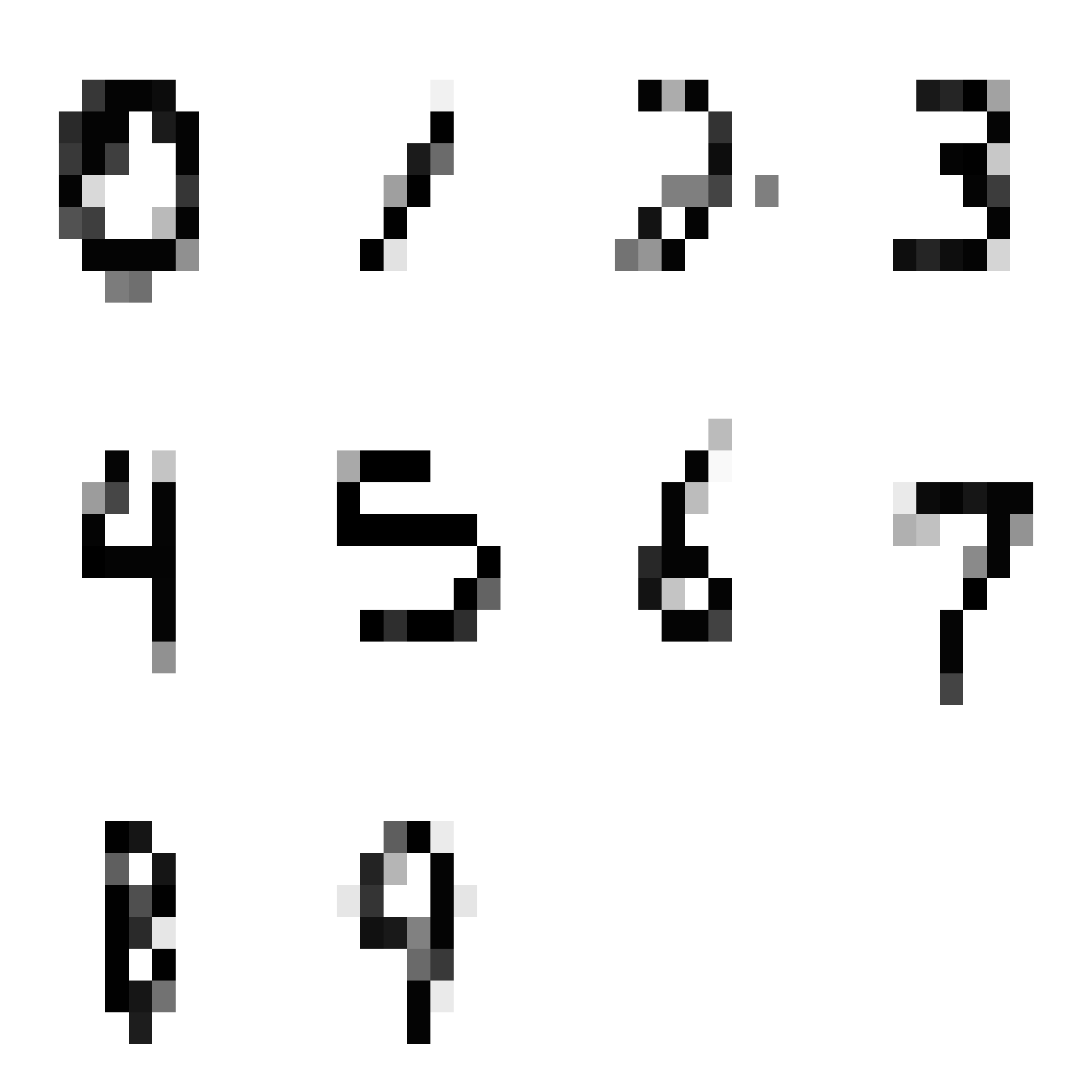
Your goal will be to try out the neuralnet package to find what kinds of network structures matter for learning to classify these digits. The representation you’ll work with is a linearized version of the digits — imagine taking all of the rows of these figures and chaining them all into one long row. This means your network won’t have any ability to use the spatial structure of the images. But even with just the pixel values, you’ll find that you can do a fair bit better than chance (\(\frac{1}{10}\)).
The neuralnet package uses what is called a one-hot encoding: The output layer will have ten nodes, each corresponding to a digit. The goal of the network when it reads say a \(9\) is for all of the output nodes except for the one corresponding to \(9\) to have no activation, and for the \(9\) node to have 1.